|
|
Correction du sujet : Bac S 1999 Polynésie (Juin 99)
Problème (11 points) Enoncé
Partie
A : 1.
a. 1. b. 2. 3. 4. 5. a. 5. b. 6.
Partie B
: 1. 2. 3. 4. 5. 6. 7. 8.
Ce sujet nécessite de
connaître les points suivants du cours :
Soit f la fonction définie sur 
par : f(x) = x - e2x -2 .
On note (C) la courbe représentative de f
dans un repère orthonormal ( O ; i , j ). On prendra 5 cm comme unité.
1. a. Déterminer la limite de f en - ¥ . (0,5 point)
On a :
donc par les théorèmes
algébriques de calcul de limite, on a
lim x®-¥ f(x) = -¥ .
1. b. Vérifier que, pour tout réel x non
nul : (0,25 point)
Déterminer la limite de f en + ¥ . (0,5 point)
On a, pour tout x positif :
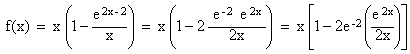
On a :
donc d'après l'expression de f
obtenue ci-dessus et d'après les théorèmes algébriques de calcul de limites, on
a :
lim x®+¥ f(x) = - ¥
2. Déterminer f ’ . Étudier le signe de f
’(x) et calculer la valeur exacte du maximum de f . (0,25 point ; 0,5 point ; 0,25 point)
f est dérivable sur R , en
tant que somme de fonctions dérivables sur 
et on a :
f ’(x) = 1 - 2e2x-2
f ’(x) = 0 ó 1 - 2e2x
-2 = 0
ó e2x –
2 = 1/2
ó ln (e2x
- 2) = ln (1/2)
ó 2x -2 = -
ln 2
ó x = 1
–(1/2)(ln 2)
f ’(x) > 0
ó 1 - 2e2x
-2 > 0
ó e2x
– 2 < 1/2
ó ln (e2x
- 2) < ln (1/2) (la fonction ln
étant strictement croissante sur ]0 ; +¥[,
l'inégalité ne change pas de sens)
ó 2x -2
< - ln 2
ó x <
1 –(1/2)(ln 2)
donc :
·
pour tout x Î
] -¥ ; 1 - (1/2)(ln 2) [, f ’( x) > 0
·
pour tout x Î ]1 -
(1/2)(ln 2) ; +¥ [, f ’(
x) < 0
·
f ’[1 - (1/2)(ln 2)] = 0 .
donc :
·
f est strictement croissante sur ] -¥ ; 1 -
(ln 2)/2 [
·
f est strictement décroissante sur ] 1 - (ln 2)/2 ; +¥ [
·
f admet un maximum en x = 1 - (ln 2)/2 .
Calculons la valeur que prend
ce maximum :
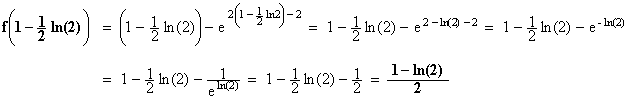
Le maximum de f sur 
est donc égal à (1-ln2)/2 .
3. Démontrer que la droite (D) d’équation
y = x est asymptote à la courbe (C). (0,5 point)
Étudier la position relative de (C) et
(D). (0,5 point)
Pour tout x réel , on a
: f(x) - x = - e2x - 2,
et on sait par la question 1.
que lim x®-¥ e2x
-2 = 0 .
donc lim x®-¥ [f(x) - x] = 0 .
On en déduit que
(D) est asymptote à (C) au voisinage de -¥.
D'autre part, pour tout x réel,
on a : e2x - 2 >
0.
donc f(x) - x < 0 ,
donc (C) est toujours située
au-dessous de (D).
4. On note A le point de la courbe (C)
d’abscisse 1.
Déterminer une équation de la tangente
(T) en A à la courbe (C). (0,5 point)
Une équation de la tangente
(T) à (C) en A est :
y = f
’(1) (x-1) + f(1)
On a :
�.
f ’(1) = 1 – 2 e2 -
2 = 1 - 2 = -1
�.
f(1) = 1 - e2 - 2 = 1 - 1
= 0
donc une équation de (T) est
: y = - x + 1 .
5. a. On note I l’intervalle [0 ; 0,5].
Démontrer que l’équation f (x) = 0
admet dans l’intervalle I une unique solution qu’on notera a. (0,5 point)
On a : 1-(1/2)(ln 2) =
0,7 à 0,1 près,
donc l'intervalle I est inclus
dans l'intervalle ] -¥ ; 1-(1/2)(ln 2) [ ,
donc f est strictement croissante
sur I.
f étant dérivable et
strictement croissante sur I, elle réalise une bijection de I sur f(I)=[f(0) ;
f(0,5)].
De plus, on a :
donc l'équation f (x) = 0 admet une unique
solution a appartenant à I.
5. b. Déterminer une valeur approchée à
10-1 près de a. (0,25
point)
Par la
calculatrice, on obtient a = 0,2 ,
à 10-1 près.
6. Construire la courbe (C), l’asymptote
(D) et la tangente (T). (0,5 point)
Partie B : Détermination
d’une valeur approchée de a
On définit dans la suite (un) par :
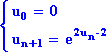
1. Soit g la fonction définie sur par g(x) = e 2x - 2 .
Démontrer que l’équation f (x) = 0
est équivalente à g(x) = x.
En déduire g(a). (0,5 point ; 0,25 point)
On a , pour tout x réel :
g(x) = x ó e2x -2
= x
ó x - e2x
- 2 = 0
ó f(x) = 0.
Comme on a f(a) = 0 , on en
déduit que :
g(a) = a
2. Démontrer que, pour tout réel x de
l’intervalle I, on a : |g'(x)| £ 2/e . (0,5 point)
La fonction g est dérivable
sur , en tant
que composée de fonctions dérivables sur .
On a , pour tout x Î , g'(x)
= 2e2x - 2 .
Or, pour tout x Î I : 0
£ x £ 1/2
ó 0 £ 2x £ 1 (2
est positif, donc le sens de l'inégalité ne change pas)
ó - 2 £ 2x - 2 £ - 1
ó e- 2
£ e2x - 2 £ e-1 (la fonction exponentielle étant strictement croissante sur R, le
sens de l'inégalité ne change pas).
ó 2/e2
£ 2.e2x - 2 £ 2/e
donc pour tout x de I, on
a |g'(x)| £ 2/e .
3. Démontrer que, pour tout réel x de
l’intervalle I, g(x) appartient à I. (0,5 point)
On a montré à la question
précédente que, pour tout x Î I, 2/e2 £ 2.e2x - 2 £ 2/e , or :
donc, pour tout x Î I, 0 £ g(x) £ 0,5 ,
donc pour tout x ÎI , g(x) appartient à I .
4. Utiliser l’inégalité des
accroissements finis pour démontrer que, pour tout entier naturel n : |un+1 - a| £ (2/e).|un
- a| . (0,75 point)
On a :
L'inégalité des accroissements
finis permet alors d'écrire que, pour tous réels x et y appartenant à I, on a
Nous devons dans un premier
temps montrer que pour tout n de 
, un appartient à I.
Procédons par récurrence :
Nous
avons un+1 = g(un) et on a montré que, pour tout réel x
de I, g (x) appartient I.
donc un+1
appartient à I.
On a donc, par récurrence, que
pour tout n de 
, un appartient à I .
L'inégalité des accroissements
finis obtenue plus haut, écrite dans le cas particulier où x = un et
y = a (a appartient bien à I) donne, pour tout n de N :
Et comme un+1 = g(un)
et g(a) = a , on obtient alors pour tout n Î :
5. Démontrer, par récurrence,
que : |un - a| £ (2/e)n . (0,75 point)
Raisonnement par récurrence :
donc
|u0 - a| £ 1 ,
donc
|u0 - a| £ (2/e)0
.
Par
l'inégalité obtenue à la question précédente, on a : |un+1 - a| £
(2/e).|un - a| ,
donc |un+1
- a| £
(2/e).(2/e)n = (2/e)n+1.
On a donc, par récurrence, que
pour tout n de ,
6. En déduire que la suite (un)
converge et donner sa limite. (0,75
point)
On a |2/e| <
1 ,
donc lim n®+¥ (2/e)n = 0 .
Par la question précédente, on
a : 0 £ |un
- a| £ (2/e) n (une valeur absolue est toujours positive !)
donc 0 £ lim n®+¥ |un - a|
£ lim n®+¥ (2/e)n = 0
donc lim n®+¥ |un - a| = 0
donc (un) converge
vers a .
7. Déterminer un entier naturel p tel
que : |up - a| < 10-5. (1 point)
On a |u p - a| < 10-5 dès que (2/e) p < 10-5 .
Or on a : (on rappelle que la
fonction logarithme étant croissante, l'inégalité ne change pas de sens !)
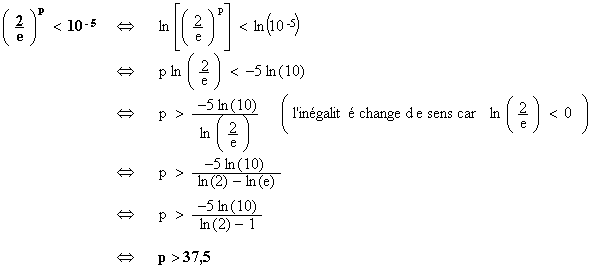
Un entier naturel p tel que |up
- a|
< 10 - 5 est
38. (Pour être précis, tous les entiers naturels supérieurs à 38 conviennent.)
8. En déduire une valeur approchée
de a
à 10-5 près : on
expliquera l’algorithme utilisé sur la calculatrice. (1 point)
Par le résultat de la question
précédente, on sait qu'une valeur approchée de
a à 10-5 près
est u 38 .
L'algorithme est simple : on
calcule u0 , puis u1 = g(u0) , … , puis un+1
= g(un) , et ce jusqu'à n =
38 au moins.
La calculatrice nous
donne u38 = 0,2031878 ,
donc une valeur approchée
de a
à 10-5 près est :
a = 0,20318
copyright
© School Angels 2009