Correction du sujet : Bac ES 1999 Polynésie (Juin 99)

Exercice 1 (4 points) Énoncé

Partie II : 1. a. 1. b. 1. c. 1. d. 2.

Ce sujet nécessite de connaître les points suivants du cours :

lecture graphique
fonction 1/f

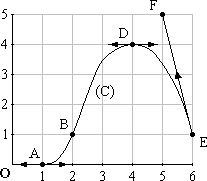
On considère une fonction f définie et dérivable sur l’intervalle [1 ; 6] . Sa courbe représentative (C) dans un repère orthogonal est donnée ci-dessous. La courbe (C) passe par les points A(1;0) , B(2;1) , D(4;4) et E(6;1) . Les tangentes à la courbe aux points A et D sont parallèles à l’axe des abscisses. La tangente à la courbe au point E passe par le point F(5;5) .

Partie I :

Par lecture graphique, résoudre l’équation f(x) = 0 et donner le signe de f(x) sur l’intervalle [1;6]. (0,5 point)

La courbe (C) coupe l’axe des abscisses en un unique point : le point A(1;0) ,

donc l’équation f(x) = 0 admet une unique solution x = 1 .

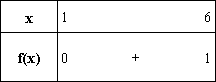
D’autre part, on observe que pour tout x appartenant à ]1;6] , (C) est au-dessus de l’axe des abscisses, d’où le tableau de signe suivant pour f(x) :

Partie II :

On désigne par g la fonction définie sur l’intervalle ]1 ; 6] par g(x) = 1/f(x) et (G) sa courbe représentative dans un repère orthonormal d’unité graphique 2 cm.

1. a. Calculer g(2), g(4) et g(6). (0,5 point)

On a :

g(2) = 1/f(2) avec f(2) = 1 d’où g(2) = 1
g(4) = 1/f(4) avec f(4) = 4 d’où g(4) = 1/4
g(6) = 1/f(6) avec f(6) = 1 d’où g(6) = 1

1. b. Déterminer la limite de g(x) quand x tend vers 1. (0,5 point)

Que peut-on en déduire pour la courbe (G) ? (0,5 point)

On a lim _x_®₁₊ f(x) = 0⁺ ,

d’où lim _x_®₁₊ g(x) = +¥ .

On en déduit que la courbe (G) représentative de la fonction g admet la droite d’équation x = 1 pour asymptote.

1. c. Dresser le tableau de variation de la fonction g sur l’intervalle ]1 ; 6] en donnant les justifications nécessaires. (1 point)

g(x) étant l’inverse arithmétique de f(x) et f(x) étant strictement positif sur ]1;6] , on en déduit que les variations de g sont les variations inverses de f , d’où :

f est strictement croissante sur l’intervalle ]1;4[ , donc g est strictement décroissante sur ]1;4[ ;
f est strictement décroissante sur l’intervalle ]4;6] , donc g est strictement croissante sur ]4;6] .

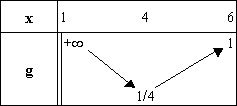
On en déduit le tableau de variations de g :

1. d. Déterminer f ' (4) ; en déduire g' (4). (0,25 + 0,25 point)

On sait que la pente de la tangente à une courbe est égale à la valeur que prend la dérivée de la fonction au point de tangence.

La courbe (C) admettant une tangente horizontale (donc de pente nulle) au point d’abscisse x = 4 ,

d’où f ’(4) = 0 .

Or, par les formules du cours, comme g = 1/f , on a g’ = - f ’/ f ² ,

d’où g’(4) = - f ’(4) / [f(4)]² (avec f(4) = 4 , donc différent de zéro),

d’où g’(4) = 0 .

2. Tracer la courbe (G) ainsi que son asymptote et la tangente au point d’abscisse 4. (0,5 point)

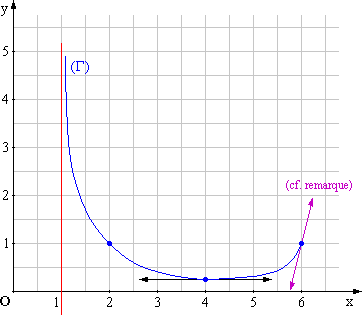
Remarque :

On peut observer sur le graphique de l’énoncé que (C) admet une tangente de pente -4 au point d’abscisse x = 6 . On peut donc en déduire que f ’(6) = -4 .

On sait donc que :

g’(x) = - f ’(x) / [f(x)]²
f ’(6) = -4
f(6) = 1

d’où g’(6) = - (-4)/1² = 4

donc g admet une tangente de pente 4 au point d’abscisse x = 6 .

Cette tangente est tracée en violet sur la figure ci-dessus.