Bac ES 1999 Polynésie (Juin 99)
Problème (12 points) Corrigé
Le
plan est rapporté à un repère orthonormal. On prendra pour unité graphique 2
cm.
On
considère les fonctions f et g définies sur l’intervalle [0 ; +¥[ par
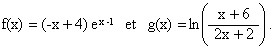
Dans
le repère choisi, on appelle (C) la courbe représentative de f et (G) la courbe représentative
de g.
1. Déterminer la limite de f
(x) quand x tend vers +¥ . (0,5
point)
2. Vérifier que la fonction
dérivée de f est définie pour tout x positif par f ’(x) = (-x+3)
ex-1 . (0,75 point)
3. Étudier le sens de
variation de la fonction f et dresser son tableau de variation. On précisera
f(0) , f ’(0) , f(3) , f ’(3) . (1,25 point)
4. Tracer la courbe (C). (1
point)
5. Déterminer les réels a et
b tels que la fonction F définie sur l’intervalle [0 ; +¥ [ par F(x) = (ax+b) ex-1 soit une primitive de la fonction f . (1
point)
On
considère la fonction u définie sur l’intervalle [0 ; +¥[ par :
![]()
1. Vérifier que, pour tout x
positif, u(x) est strictement positif.
(0,5 point)
2.
a.
Déterminer la limite de u(x) quand x tend vers +¥ . (0,5 point)
2.
b. Étudier
le sens de variation de u . (0,5
point)
Dresser
le tableau de variation de u et retrouver le résultat de la question 1.
de la Partie B . (0,5 point)
3. En utilisant les résultats
précédents, déterminer le sens de variation de la fonction g et démontrer que
la courbe (G) admet une asymptote (D) au voisinage de +¥ dont on donnera une équation. (1 point)
4. Tracer la courbe (G) et la droite (D) sur le
même graphique que celui de la partie A . (0,75 point)
5. Soit G la fonction définie
sur l’intervalle [0 ; +¥[ par :
G(x)
= (x+6) ln(x+6) -
(x+1) ln(2x+2) .
Démontrer
que G est une primitive de la fonction g sur l’intervalle [0 ; +¥[ . (0,75 point)
1. Résoudre, à l’aide des
représentations graphiques faites, l’inéquation g(x) £ f(x) . (1
point)
2. Calculer l’aire A en cm2 du domaine du plan constitué des points M( x ;
y) tels que :
2 £ x £ 3 et g(x) £ y £ f (x) . (1
point)
Donner
l’arrondi de A à l’unité près. (1 point)
copyright © School Angels 2000