Bac ES 1999 Asie
(Juin 99)
Exercice 2 (6 points) SPECIALITE Corrigé
Dans l’espace rapporté au
repère orthonormal (O ; i , j , k ) , on a placé les
points : (voir annexes 1 et 2)
- A (0 ;
0 ; 18)
- B (0 ;
15 ; 0)
- C (22,5 ;
0 ; 0)
- D (0 ; 0 ; 12,5)
- E (0 ; 25 ; 0)
- F (12,5 ; 0 ; 0)
Le plan (ABC) a pour équation : 4x + 6y + 5z =
90.
Le plan (DFE) a pour équation : 2x + y + 2z =
25.
La droite (GI) est l’intersection des plans (ABC) et
(DFE).
On admet que tout point M (x ; y ; z)
appartenant au polyèdre ODGBIF a des coordonnées qui satisfont aux
conditions :
- x ³ 0
- y ³ 0
- z ³ 0
- 4x + 6y + 5z £ 90
- 2x + y + 2z £ 25
Une usine fabrique 3 types de vannes pour
l’industrie pétrolière.
Pour fabriquer le modèle V1, il faut 20 heures d’usinage et 20 heures de
montage.
Pour fabriquer le modèle V2, il faut 30 heures d’usinage et 10 heures de
montage.
Pour fabriquer le modèle V3, il faut 25 heures d’usinage et 20 heures de
montage.
Le nombre d’ouvriers spécialisés permet de disposer
de 450 heures d’usinage par semaine.
Le nombre d’ouvriers monteurs permet de disposer de
250 heures de montage par semaine.
On désigne par x le nombre de vannes de type V1 fabriquées dans une semaine, y le nombre de vannes
de type V2 et z le nombre de vannes de
type V3.
Les points de coordonnées (x ; y ; z) qui
satisfont aux contraintes précédentes sont situés à l’intérieur du polyèdre
ODGBIF.
Le bénéfice réalisé sur une vanne de type V1 est de 2 000 F, sur une vanne de type V2, il est de 3000 F et enfin sur une vanne de type V3, il est de 5000 F.
Un point de coordonnées (x ; y ; z)
représente une production.
Questions :
a. Montrez que les points représentant une production
pour laquelle le bénéfice total est de 30000 F sont situés sur le plan (P)
d’équation cartésienne 2x + 3y + 5z = 30.
(1 point)
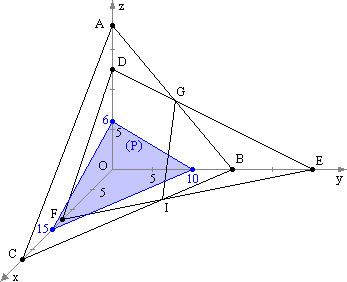
Le plan (P) est tracé sur la figure de l’annexe 2
.
b. Montrez qu’une production de 5 vannes de type V1, de 5 vannes de type V2 et d’une vanne de type V3 est réalisable par cette usine en une semaine et
que le bénéfice alors réalisé est de 30000 F . (1 point)
Quelle conclusion en tirez-vous sur la position du point
K de coordonnées (5 ; 5 ; 1) ?
(1 point)
c. Montrez que les points représentant une production
pour laquelle le bénéfice total est de 60000 F sont situés sur le plan (Q)
d’équation cartésienne : 2x + 3y + 5z = 60 . (1 point)
d. Quelle remarque pouvez-vous faire sur les plans (P)
et (Q) ? (1 point)
e. On admet que le bénéfice réalisé par l’entreprise
est maximal lorsque le plan (R) d’équation
2x + 3y + 5z = b passe par le
point G dont les coordonnées sont : (0 ; 55/7 ; 60/7 ) .
Calculer ce bénéfice maximal. (1
point)
Annexe 1

Annexe 2
copyright © School Angels 2000